Yixin Ou (欧翌昕)

I am now a second-year Master student of ZJUNLP majored in Computer Science and Technology at Zhejiang University, advised by Huajun Chen (陈华钧) and Ningyu Zhang (张宁豫). Previously, I graduated from the College of Computer Science and Technology, Zhejiang University (浙江大学计算机科学与技术学院) with a bachelor’s degree.
My current research interests focus on Large Language Models (LLMs) and their theory and applications. I’m interested in the Mechanism Interpretability of LLMs and the application of LLMs to Autonomous Agents. I have published 5+ papers 
I will graduate in the spring of 2026 and I’m seeking a job position as a researcher or engineer of LLM algorithm.
News
| Jun 16, 2025 | Start my internship at Meituan. |
|---|---|
| May 16, 2025 | Our paper Dynamics of Knowledge Circuits is accepted by ACL 2025 (Findings)! 🎉 |
| Mar 06, 2025 | Our paper Dynamics of Knowledge Circuits is accepted by SCI-FM @ ICLR 2025! 🎉 |
| Jul 02, 2024 | Start my internship at Huawei Noah’s Ark Lab under the supervision of Hui Jin and Jiacheng Sun. |
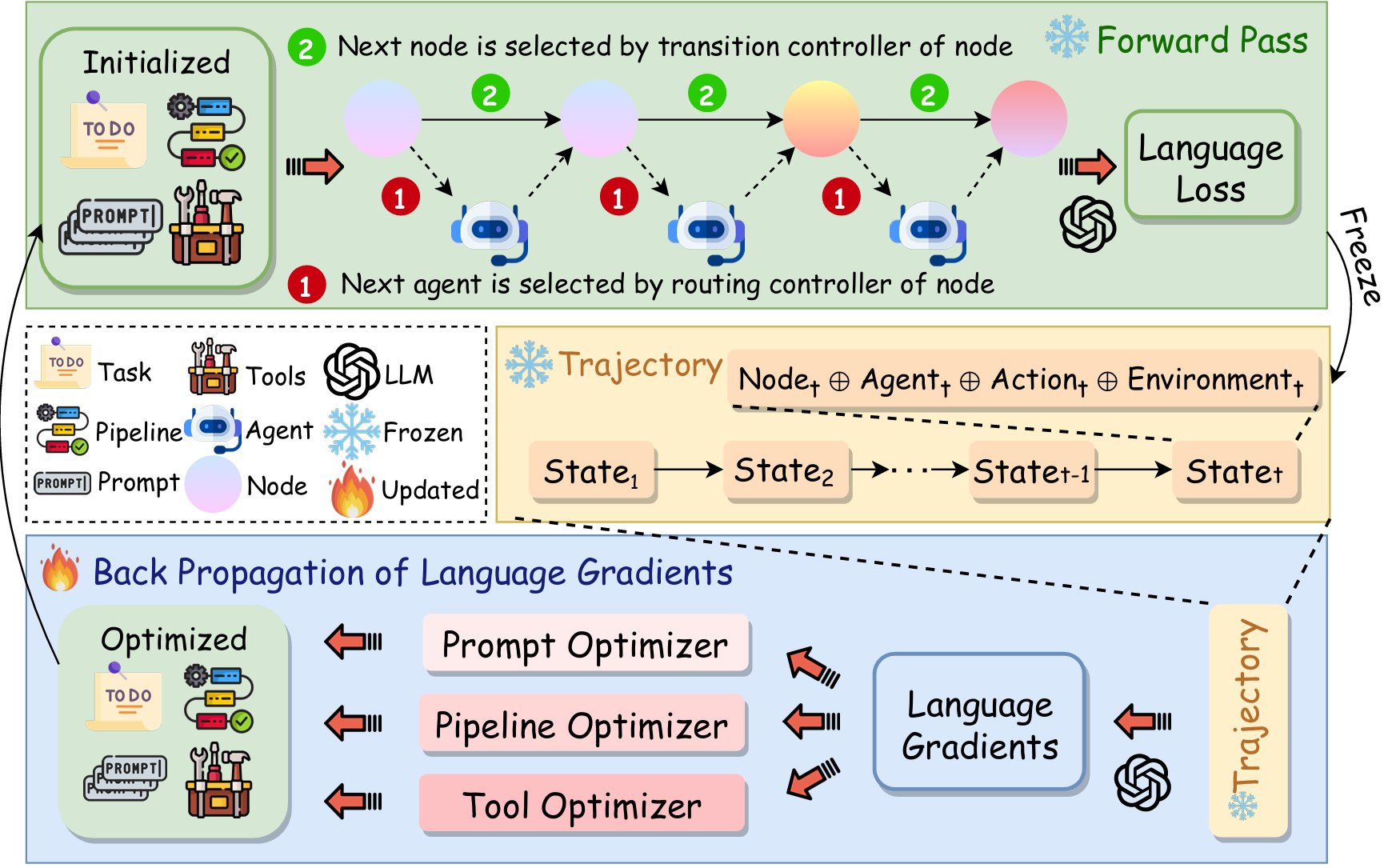
| Jun 25, 2024 | We release our new work Agent Symbolic Learning. Thanks for the supervision of Wangchunshu Zhou. |
Selected Publications
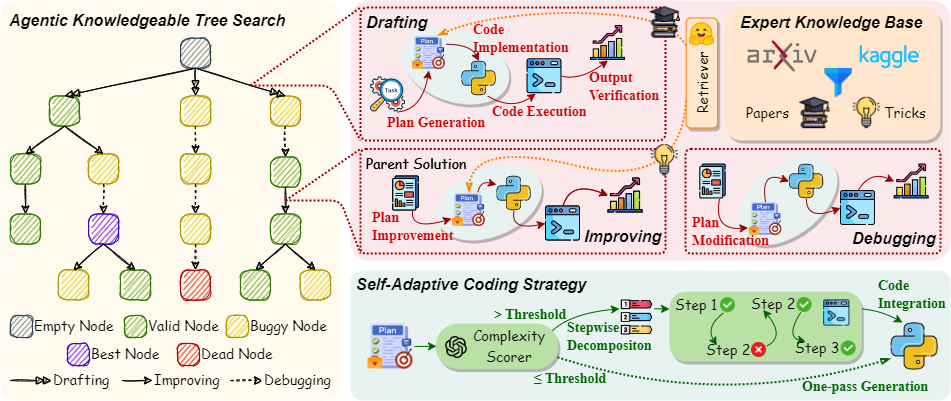
- Preprint
- The 63rd Annual Meeting of the Association for Computational Linguistics (Findings), Feb 2025
- Preprint
- 2025 Annual Conference of the Nations of the Americas Chapter of the Association for Computational Linguistics (Findings), Mar 2024
- The 62nd Annual Meeting of the Association for Computational Linguistics (System Demonstration Track), Feb 2024
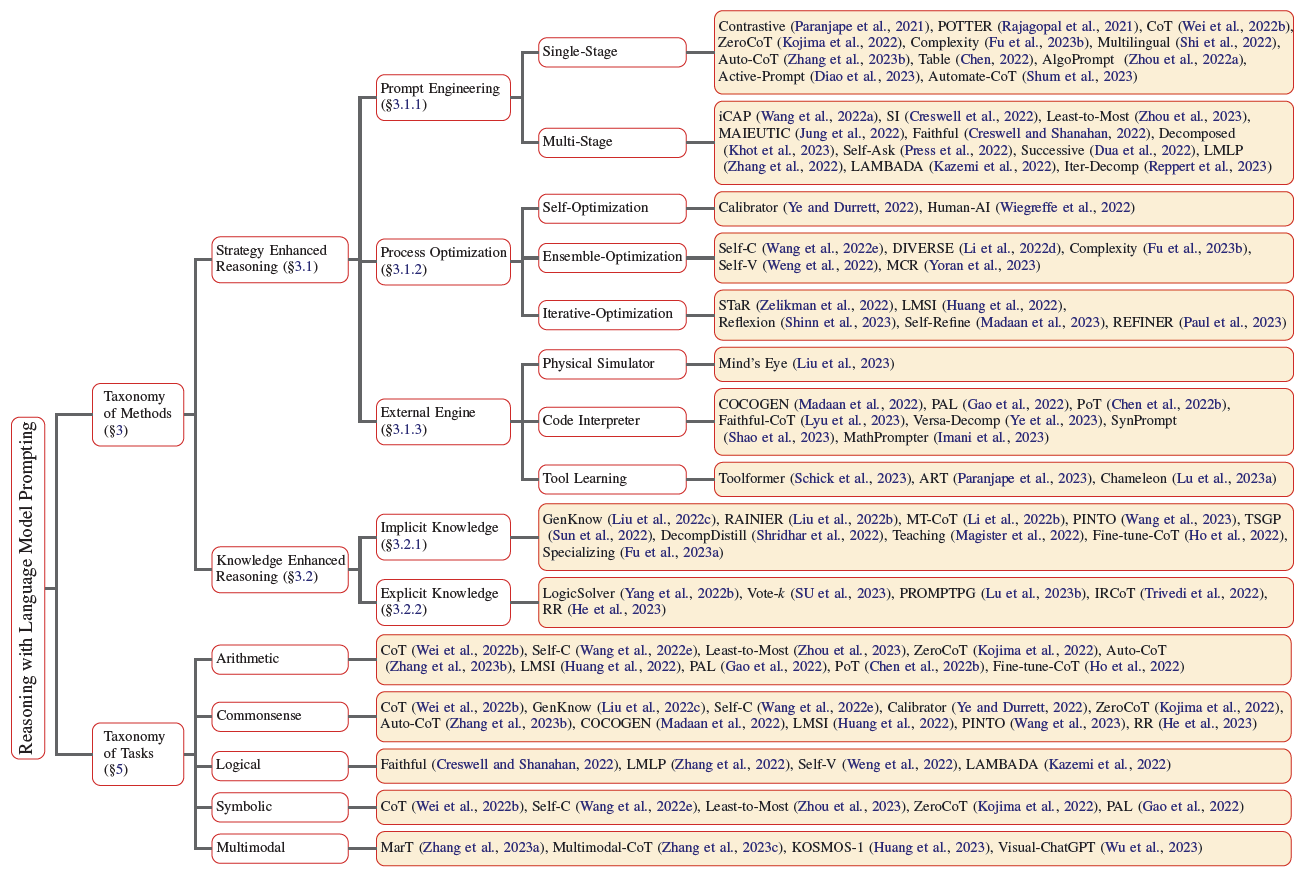
- The 62nd Annual Meeting of the Association for Computational Linguistics, Oct 2023
- The 61st Annual Meeting of the Association for Computational Linguistics, Dec 2022