AVL Trees, Splay Trees and Amortized Analysis

AVL Trees

• Target: Speed up searching (with insertion and deletion)
• Tool: Binary search trees
• Problem: Although $T_p = O( \text{height} )$, but the height can be as bad as $O( N )$

[Definition] An empty binary tree is height balanced. If $T$ is a nonempty binary tree with $T_L$ and $T_R$ as its left and right subtrees, then $T$ is height balanced if and only if

• $T_L$ and $T_R$ are height balanced, and
• $| h_L - h_R | \leq 1$ where $h_L$ and $h_R$ are the heights of $T_L$ and $T_R$ , respectively.

Note: The height of an empty tree is defined to be -1, and the height of a single node is defined to be 0.

[Definition] The balance factor $BF( node ) = h_L - h_R$. In an AVL tree, $BF( node ) = -1, 0, or 1$.

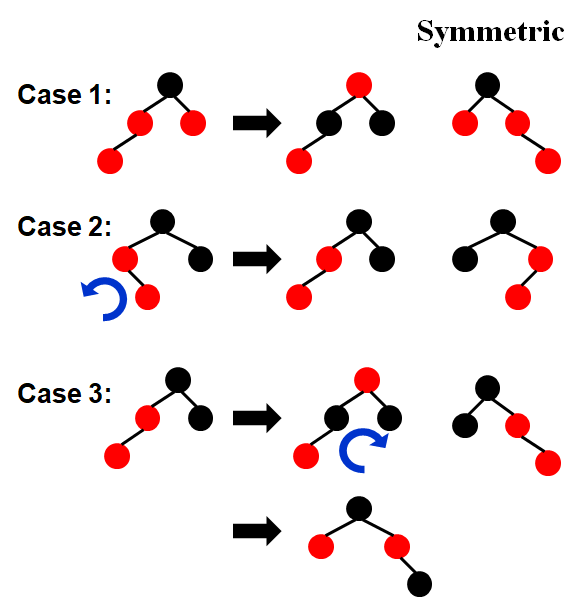
Single Rotation

RR Rotation

LL Rotation

Double Rotation

LR Rotation

RL Rotation

Conclusion

• Single Rotation中RR对应一次逆时针，LL对应一次顺时针
• Double Rotation中从后往前读，R对应一次逆时针，L对应一次顺时针
  • LR先逆时针再顺时针
  • RL先顺时针再逆时针

Note: Several bf’s might be changed even if we don’t need to reconstruct the tree.

The correct answer is A.

The height of AVL Tree

Splay Trees

• Target: Any $M$ consecutive tree operations starting from an empty tree take at most $O(M \log N)$ time.

Note: AVL Tree is a kind of Splay Tree because every operation takes $O(\log N)$ time.

• Splay Tree only means that the amortized time is $O(\log N)$. A single operation might still take $O(N)$ time.
• The bound is weaker. But the effect is the same: There are no bad input sequences.
• Whenever a node is accessed, it must be moved to avoid the case of successive operations taking $O(N)$ time.
• Idea: After a node is accessed, it is pushed to the root by a series of AVL tree rotations.

A simple solution

• Only use single rotation

• The time complexity of the worst case might be $O(N^2)$, so it doesn’t work.

Splaying

Note: The operation order of one Zig-zig is from up to down.

• Splaying not only moves the accessed node to the root, but also roughly halves the depth of most nodes on the path.

Deletions

• Step1: Find X and X will be at the root
• Step2: Remove X and there will be two subtrees $T_L$ and $T_R$
• Step3: $FindMax ( T_L ) $ and the largest element will be the root of $T_L$ , and has no right child
• Step4: Make $T_R$ the right child of the root of $T_L$

Amortized Analysis 摊还分析

• Target: Any $M$ consecutive operations take at most $O(M \log N)$ time. — Amortized time bound
• worst-case bound $\geq$ amortized bound $\geq$ average-case bound
• Probability is not involved in amortized bound
• 摊还分析可以保证最坏情况下每个操作的平均性能

Aggregate analysis 聚合分析

• Idea: Show that for all $n$, a sequence of $n$ operations takes worst-case time $T(n)$ in total. In the worst case, the average cost, or amortized cost, per operation is therefore $T(n)/n$.

• We can pop each object from the stack at most once for each time we have pushed it onto the stack

Accounting method 核算法

• Idea: When an operation’s amortized cost $\hat c_i$ exceeds its actual cost $c_i$, we assign the difference to specific objects in the data structure as credit. Credit can help pay for later operations whose amortized cost is less than their actual cost.

• The difference between aggregate analysis and accounting method is that the later one assumes that the amortized costs of the operations may differ from each other

• For all sequences of $n$ operations, we have

  $\sum^n_{i=1}\hat c_i\geq \sum^n_{i=1}c_i$

  $T_{amortized}=\frac{\sum^n_{i=1}\hat c_i}{n}$

Potential method 势能法

• Idea: Take a closer look at the credit : $\hat c_i-c_i=\text{Credit}_i=\Phi(D_i)-\Phi(D_{i-1})$
• $D_i$ id defined to be the structure of the current situation
• Potential function maps the current structure of the problem into a number

$\hat c_i=c_i+\Phi(D_i)-\Phi(D_{i-1})\\ \sum^n_{i=1}\hat c_i=\sum^n_{i=1}(c_i+\Phi(D_i)-\Phi(D_{i-1}))=\sum^n_{i=1}c_i+\Phi(D_n)-\Phi(D_0)$

• A good potential function should always assume its minimum at the start of the sequence

Splay Trees势能分析

• 势能函数是树中所有节点的 rank 之和

  $\Phi(T)=\sum^n_{i=1}R(i)=\sum^n_{i=1}\log S(i)$

  其中$S(i)$指的是子树$i$中的节点数(包括节点$i$)，用$R(i)$表示节点 $i$ 的 rank，$R(i)=\log S(i)$

• 用$R_2$表示操作后的势能，$R_1$表示操作前势能

• zig
  • 实际成本是一次单旋，为1
  • 只有 $X$ 和 $P$ 的 rank 值有变化，故$\hat c_i = 1 + R_2(X) − R_1(X) + R_2(P) − R_1(P)$
  • 节点 $P$ 由根节点变为非根节点，故$R_2(P)-R_1(P)\leq0$，因此$\hat c_i\leq 1+R_2(X)-R_1(X)\leq 1+3(R_2(X)-R_1(X))$
• zig-zag

  • 实际成本是两次旋转，为2

  • $\hat c_i = 2 + R_2(X) − R_1(X) + R_2(P) − R_1(P)+R_2(G) − R_1(G)$

  • 操作前$G$是根节点，操作后$X$是根节点，rank相同，故$\hat c_i = 2− R_1(X) + R_2(P) − R_1(P)+R_2(G)$

  • $R_1(P)\geq R_1(X)$

  • $S_2(P)+S_2(G)\leq S_2(X)$，根据定理可得$R_2(P)+R_2(G)\leq 2R_2(X)-2$

  • $\hat c_i = 2− R_1(X) + R_2(P) − R_1(P)+R_2(G)\leq 2 + R_2(P)+R_2(G)− 2R_1(X)\\ \leq 2 + R_2(P)+R_2(G)− 2R_1(X)-(R_2(P)+R_2(G)− 2R_2(X)+2)=2(R_2(X)-R_1(X))$

• zig-zig
  • 实际成本是两次单旋，为2
  • $\hat c_i = 2 + R_2(X) − R_1(X) + R_2(P) − R_1(P)+R_2(G) − R_1(G)$
  • 操作前$G$是根节点，操作后$X$是根节点，rank相同，故$\hat c_i = 2− R_1(X) + R_2(P) − R_1(P)+R_2(G)$
  • $R_1(P)\geq R_1(X)$
  • $R_2(G)\leq R_2(P)\leq R_2(X)$
  • $\hat c_i\leq2(R_2(X)-R_1(X))+2\leq3(R_2(X)-R_1(X))$
• [Theorem] The amortized time to splay a tree with root $T$ at node $X$ is at most $3( R( T ) – R ( X ) ) + 1 = O(\log N)$.