Rationale of the Backtracking Algorithms

  • A sure-fire way to find the answer to a problem is to make a list of all candidate answers, examine each, and following the examination of all or some of the candidates, declare the identified answer

  • If the list is finite and it is possible to identify the answer following the examinations. And, if there are not too many candidates

  • Backtracking enables us to eliminate the explicit examination of a large subset of the candidates while still guaranteeing that the answer will be found if the algorithm is run to termination

  • pruning(剪枝)

  • The basic idea is that suppose we have a partial solution (x1,⋯ ,xi)( x_1, \cdots , x_i ) where each xk∈Skx_k \in S_k for 1≤k≤i<n1 \leq k \leq i < n. First we add xi+1∈Si+1x_{i+1}\in S_{i+1} and check if (x1,⋯ ,xi,xi+1)( x_1, \cdots , x_i ,x_{i+1}) satisfies the constrains. If the answer is “yes” we continue to add the next x, else we delete xix_i and backtrack to the previous partial solution (x1,⋯ ,xi−1)( x_1, \cdots , x_{i-1} )

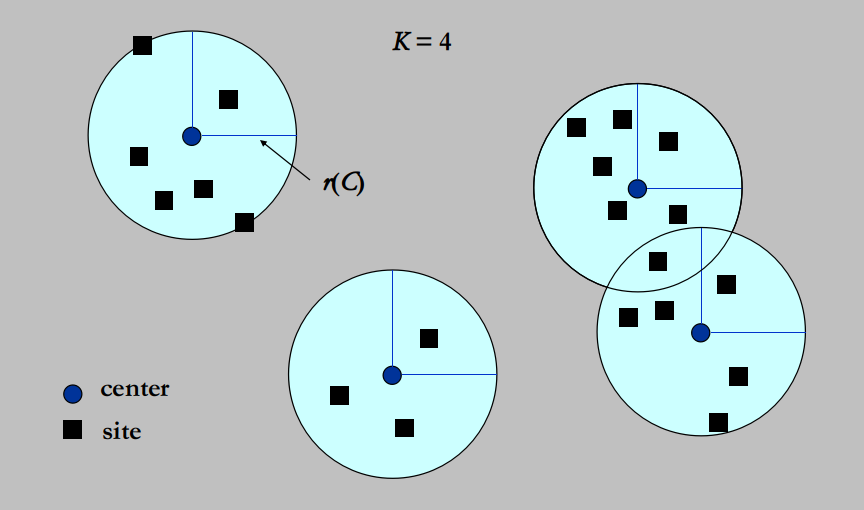
Eight Queens

  • Find a placement of 8 queens on an 8×88 \times 8 chessboard such that no two queens attack
  • Two queens are said to attack if they are in the same row, column, diagonal, or antidiagonal of the chessboard
image-20210416101814796

  • Constraints

    • Si={1,2,3,4,5,6,7,8}S_i=\{1,2,3,4,5,6,7,8\} for 1≤i≤81\leq i\leq 8

      Note: This implies 888^8 candidates in the solution space

    • xi≠xjx_i\neq x_j if i≠ji\neq j

      Note: This implies that the solution must be a permutation of 1,2,⋯ ,81, 2, \cdots , 8. Thus the number of candidates in the solution space is reduced to 8!8!

    • (xi−xj)/(i−j)≠±1(x_i-x_j)/(i-j)\neq \pm 1

  • For the problem with nn queens, there are n!n! candidates in the solution space

  • Method: Take the problem of 4 queens as an example

    • Step1: Construct a game tree

      image-20210416110032904

      Each path from the root to a leaf defines an element of the solution space

    • Step2: Each path from the root to a leaf defines an element of the solution space

      image-20210416110148418

      image-20210416110709551

      Note: No tree is actually constructed. The game tree is just an abstract concept

The Turnpike Reconstruction Problem

  • Given NN points on the x-axis with coordinates x1<x2<⋯<xNx_1 < x_2 <\cdots < x_N . Assume that x1=0x_1 = 0. There are N(N–1)/2N ( N – 1 ) / 2 distances between every pair of points
  • Given N(N–1)/2N ( N – 1 ) / 2 distances. Reconstruct a point set from the distances
image-20210416121810728 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
bool Reconstruct (DistType X[ ], DistSet D, int N, int left, int right)
{ /* X[1]...X[left-1] and X[right+1]...X[N] are solved */
	bool Found = false;
    if (Is_Empty(D))
        return true; /* solved */
    D_max = Find_Max(D);
    /* option 1：X[right] = D_max */
    /* check if |D_max-X[i]| in D is true for all X[i]’s that have been solved */
    OK = Check( D_max, N, left, right ); /* pruning */
    if (OK) /* add X[right] and update D */
    { 
        X[right] = D_max;
        for (i=1; i<left; i++) Delete(|X[right]-X[i]|, D);
        for (i=right+1; i<=N; i++) Delete(|X[right]-X[i]|, D);
        Found = Reconstruct(X, D, N, left, right-1);
        if (!Found) 
        { /* if does not work, undo */
            for (i=1; i<left; i++) Insert(|X[right]-X[i]|, D);
            for (i=right+1; i<=N; i++) Insert(|X[right]-X[i]|, D);
        }
    }
    /* finish checking option 1 */
    if (!Found) /* if option 1 does not work */
    { 
        /* option 2: X[left] = X[N]-D_max */
        OK = Check(X[N]-D_max, N, left, right);
        if (OK) 
        {
            X[left] = X[N]–D_max;
            for (i=1; i<left; i++) Delete(|X[left]-X[i]|, D);
            for (i=right+1; i<=N; i++) Delete(|X[left]-X[i]|, D);
            Found = Reconstruct (X, D, N, left+1, right);
            if (!Found) 
            {
                for (i=1; i<left; i++) Insert(|X[left]-X[i]|, D);
                for (i=right+1; i<=N; i++) Insert(|X[left]-X[i]|, D);
            }
        }
        /* finish checking option 2 */
    } /* finish checking all the options */  
    return Found;
}

A Template

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
bool Backtracking (int i)
{   
	Found = false;
    if (i > N) return true; /* solved with (x1, …, xN) */
    for ( each xi in Si ) /* check if satisfies the restriction R */
    { 
        OK = Check((x1, …, xi) , R); /* pruning */
        if ( OK ) 
        {
            Count xi in;
            Found = Backtracking(i+1);
            if (!Found) Undo( i ); /* recover to (x1, …, xi-1) */
        }
        if (Found) break; 
    }
    return Found;
}

  • 回溯的效率跟S的规模、约束函数的复杂性、满足约束条件的结点数相关

  • 约束函数决定了剪枝的效率，但是如果函数本身太复杂也未必合算

  • 满足约束条件的结点数最难估计，使得复杂度分析很难完成

  • When different SiS_i’s have different sizes

    image-20210416122937045

    Smaller SiS_i first so we can cut a larger subtree if one doesn’t work

image-20210510010021467

Tic-tac-toe

  • The player who succeeds in placing three of their marks in a horizontal, vertical, or diagonal row wins the game.
image-20210416154331024

Minimax Strategy

  • Use an evaluation function to quantify the “goodness” of a position

    f(P)=WComputer−WHumanf(P)=W_{Computer}-W_{Human}

    where WW is the number of potential wins at position PP

    image-20210416154618355

  • The human is trying to minimize the value of the position PP, while the computer is trying to maximize it

image-20210416155036395

α\alpha pruning

image-20210416155440388

β\beta pruning

image-20210416155534378

α\alpha-β\beta pruning

  • When both α\alpha pruning and betabeta pruning techniques are combined
  • In practice, it limits the searching to only O(N)O(\sqrt N) nodes, where NN is the size of the full game tree