Greedy Method

Introduction

Optimization Problems: Given a set of constraints and an optimization function. Solutions that satisfy the constraints are called feasible solutions. A feasible solution for which the optimization function has the best possible value is called an optimal solution.
The Greedy Method: Make the best decision at each stage, under some greedy criterion. A decision made in one stage is not changed in a later stage, so each decision should assure feasibility.

Note:

Greedy algorithm works only if the local optimum is equal to the global optimum.

Greedy algorithm does not guarantee optimal solutions. However, it generally produces solutions that are very close in value (heuristics) to the optimal, and hence is intuitively appealing when finding the optimal solution takes too much time.

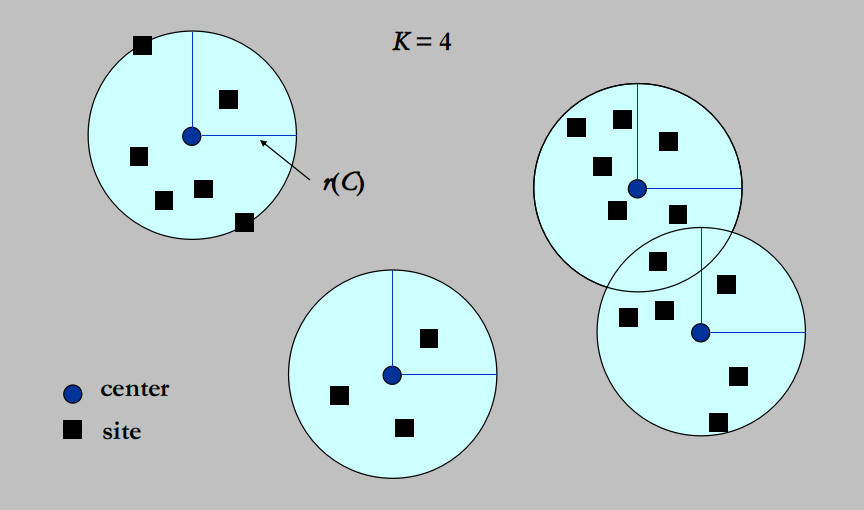
Activity Selection Problem

Given a set of activities $S = { a_1, a_2, \cdots, a_n }$ that wish to use a resource. Each $a_i$ takes place during a time interval $[s_i, f_i)$ .
Activities $a_i$ and $a_j$ are compatible if $s_i \geq f_j$ or $s_j \geq f_i$ (i.e. their time intervals do not overlap).
Target: Select a maximum-size subset of mutually compatible activities.

Greedy criterion

Greedy Rule 1

Select the interval which starts earliest (but not overlapping the already chosen intervals)
Counterexample:

Greedy Rule 2

Select the interval which is the shortest (but not overlapping the already chosen intervals)
Counterexample:

Greedy Rule 3

Select the interval with the fewest conflicts with other remaining intervals (but not overlapping the already chosen intervals)
Counterexample:

Greedy Rule 4

Select the interval which ends first or starts latest (but not overlapping the already chosen intervals)
Resource become free as soon as possible
Correctness:
- Algorithm gives non-overlapping intervals
- The result is optimal

[Theorem] Consider any nonempty subproblem $S_k$ , and let $a_m$ be an activity in $S_k$ with the earliest finish time. Then $a_m$ is included in some maximum-size subset of mutually compatible activities of $S_k$ .

Proof:
- Let $A_k$ be the optimal solution set, and $a_{ef}$ is the activity in $A_k$ with the earliest finish time.
- If $a_m$ and $a_{ef}$ are the same, we are done, else replace $a_{ef}$ by $a_m$ and get $A_k’$ .
- Since $f_m \leq f_{ef}$ , $A_k’$ is another optimal solution.
Implementation:
- Select the first activity; Recursively solve for the rest.
- Remove tail recursion by iterations.
- $T(N)=O(N\log N)$ to sort the end time or start time.

Elements of the Greedy Strategy

Cast the optimization problem as one in which we make a choice and are left with one subproblem to solve.
Prove that there is always an optimal solution to the original problem that makes the greedy choice, so that the greedy choice is always safe.
Demonstrate optimal substructure by showing that, having made the greedy choice, what remains is a subproblem with the property that if we combine an optimal solution to the subproblem with the greedy choice we have made, we arrive at an optimal solution to the original problem.

Note: Beneath every greedy algorithm, there is almost always a more cumbersome(麻烦的) dynamic-programming solution

Huffman Codes

Note: If all the characters occur with the same frequency, then there are not likely to be any savings.

If character $C_i$ is at depth $d_i$ and occurs $f_i$ times, then the cost of the code = $\sum d_i f_i$ .

The trick is: No code is a prefix of another.
Any sequence of bits can always be decoded unambiguously if the characters are placed only at the leaves of a full tree(all nodes are leaves or have two children), such kind of code is called prefix code.

Huffman’s Algorithm

void Huffman ( PriorityQueue  heap[ ],  int  C )
{   consider the C characters as C single node binary trees,
     and initialize them into a min heap;
     for ( i = 1; i < C; i++ ) { 
        create a new node;
        /* be greedy here */
        delete root from min heap and attach it to left_child of node;
        delete root from min heap and attach it to right_child of node;
        weight of node = sum of weights of its children;
        /* weight of a tree = sum of the frequencies of its leaves */
        insert node into min heap;
   }
}