Local Search

Introduction

Solve problems approximately - aims at a local optimum

Framework of Local Search

Local
- Define neighborhoods in the feasible set
- A local optimum is a best solution in a neighborhood
Search
- Start with a feasible solution and search a better one within the neighborhood
- A local optimum is achieved if no improvement is possible

Neighbor Relation

S ~ S’: S’ is a neighboring solution of S, S’ can be obtained by a small modification of S
N(S): neighborhood of S, the set { S’: S ~ S’ }

梯度下降法

SolutionType Gradient_descent()
{   
	Start from a feasible solution S in FS ;
    MinCost = cost(S);
    while (1) 
    {
        S’ = Search(N(S)); /*find the best S’ in N(S)*/
        CurrentCost = cost(S’);
        if ( CurrentCost < MinCost ) 
        {
            MinCost = CurrentCost;    
            S = S’;
        }
        else  break;
    }
    return S;
}

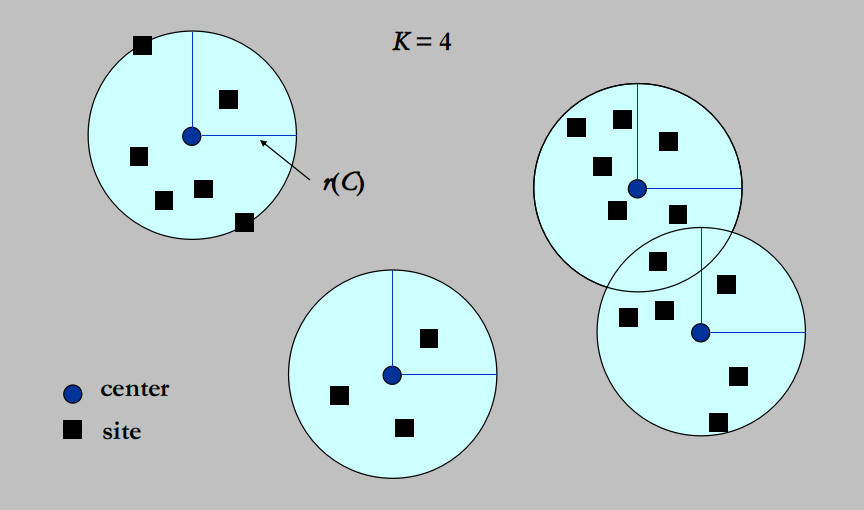
Vertex Cover

Vertex cover problem: Given an undirected graph $G = (V, E)$ and an integer $K$ , does $G$ contain a subset $V' \subseteq V$ such that $|V'|$ is (at most) $K$ and every edge in $G$ has a vertex in $V'$ (vertex cover)?
Vertex cover problem: Given an undirected graph $G = (V, E)$ . Find a minimum subset $S$ of $V$ such that for each edge $(u, v)$ in $E$ , either $u$ or $v$ is in $S$ .
Feasible solution set FS : all the vertex covers. $V\in FS$
$cost(S)=|S|$
S ~ S’: S’ can be obtained from S by (adding or) deleting a single node.

Each vertex cover S has at most $|V|$ neighbors.
Search: Start from $S = V$ ; delete a node and check if S’ is a vertex cover with a smaller cost.

The Metropolis Algorithm

SolutionType Metropolis()
{   
	Define constants k and T;
    Start from a feasible solution S in FS ;
    MinCost = cost(S);
    while (1) 
    {
        S’ = Randomly chosen from N(S); 
        CurrentCost = cost(S’);
        if ( CurrentCost < MinCost ) 
        {
            MinCost = CurrentCost;    
            S = S’;
        }
        else 
        {
            With a probability e^(-△cost/ (kT)), let S = S’;
            else  break;
        }
    }
    return S;
}

Simulated Annealing

The material is cooled very gradually from a high temperature, allowing it enough time to reach equilibrium at a succession of intermediate lower temperatures.
Cooling schedule: $T = \{ T_1 , T_2 , \cdots \}$

Hopfield Neural Networks

Definitions

Graph $G = (V, E)$ with integer edge weights $w$ (positive or negative).
If $w_e < 0$ , where $e = (u, v)$ , then $u$ and $v$ want to have the same state; if $w_e > 0$ then $u$ and $v$ want different states.
The absolute value $|w_e|$ indicates the strength of this requirement.
Output: A configuration $S$ of the network – an assignment of the state $s_u$ to each node $u$
There may be no configuration that respects the requirements imposed by all the edges.
Object: Find a a configuration that is sufficiently good.

[Definition] In a configuration $S$ , edge $e = (u, v)$ is good if $w_e s_u s_v < 0$ ( $w_e < 0$ iff $s_u = s_v$ ); otherwise, it is bad.

[Definition] In a configuration $S$ , a node $u$ is satisfied if the weight of incident good edges $\geq$ weight of incident bad edges.

$\sum_{v:e(u,v)\in E}w_es_us_v\leq0$

[Definition]A configuration is stable if all nodes are satisfied.

State-flipping Algorithm

ConfigType State_flipping()
{
    Start from an arbitrary configuration S;
    while ( ! IsStable(S) ) 
    {
        u = GetUnsatisfied(S);
        su = - su;
    }
    return S;
}

The state-flipping algorithm terminates at a stable configuration after at most $W = \sum_e|w_e|$ iterations.

Problem: To maximize $\Phi$ .
Feasible solution set FS : configurations
S ~ S’: S’ can be obtained from S by flipping a single state
Any local maximum in the state-flipping algorithm to maximize $\Phi$ is a stable configuration.
Still an open question: to find an algorithm that constructs stable states in time polynomial in $n$ and $\log W$ (rather than $n$ and $W$ ), or in a number of primitive arithmetic operations that is polynomial in $n$ alone, independent of the value of $W$ .

Maximum Cut

The Maximum Cut problem

Given an undirected graph $G = (V, E)$ with positive integer edge weights we, find a node partition (A, B) such that the total weight of edges crossing the cut is maximized.
$w(A,B)=\sum_{u\in A,v\in B}w_{uv}$

Problem: To maximize $\Phi(S)=\sum_{\text{e is good}}|w_e|$
Feasible solution set FS: any partition $(A, B)$
S ~ S’: S’ can be obtained from S by moving one node from $A$ to $B$ , or one from $B$ to $A$ .
A special case of Hopfield Neural Network – with we all being positive.

ConfigType State_flipping()
{
    Start from an arbitrary configuration S;
    while ( ! IsStable(S) ) 
    {
        u = GetUnsatisfied(S);
        su = - su;
    }
    return S;
}

May NOT in polynomial time

Quality of Local Optimum

Let $(A, B)$ be a local optimal partition and let $(A*, B*)$ be a global optimal partition. Then $w(A, B) \geq \frac12 w(A*, B*)$ .

Big-improvement-flip

Stop the algorithm when there are no “big enough” improvements.
Big-improvement-flip: Only choose a node which, when flipped, increases the cut value by at least

$\frac{2\epsilon}{|V|}w(A,B)$
Upon termination, the big-improvement-flip algorithm returns a cut $(A, B)$ so that

$(2+\epsilon)w(A,B)\geq w(A*,B*)$
The big-improvement-flip algorithm terminates after at most $O(n/\epsilon\log W)$ flips

Try a better “local”

The neighborhood of a solution should be rich enough that we do not tend to get stuck in bad local optimal; but the neighborhood of a solution should not be too large, since we want to be able to efficiently search the set of neighbors for possible local moves.
Single-flip -> k-flip -> $\Theta(n^k)$ for searching in neighbors