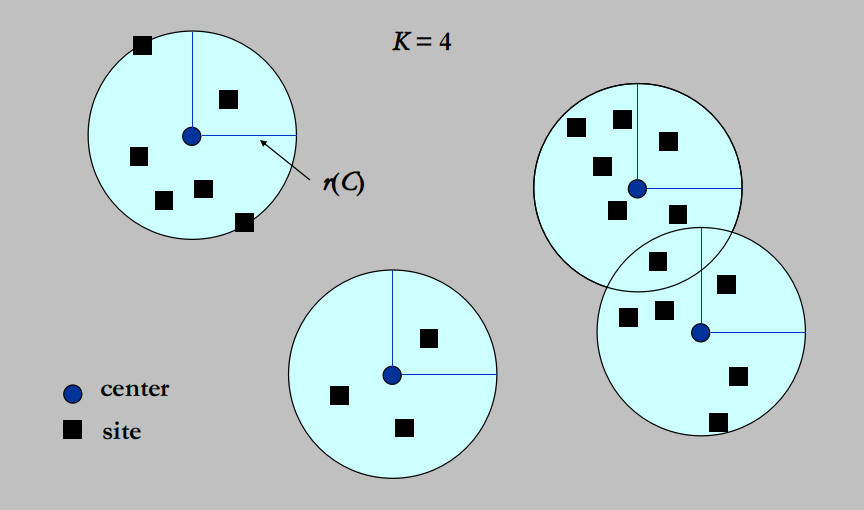
NP-Completeness
-
NP 类问题指在多项式时间内可以被证明的问题
-
所有的 P 类问题同时也是 NP 类问题,即
-
P 类问题是否是 NP 类问题的真子集在目前是一个开放问题
-
如果一个 NP 问题和其它任何 NP 问题一样“不易解决”,则认为这一问题是 NP 完全问题
-
如果任何 NP 完全问题可以在多项式时间内解决,则所有 NP 问题都有一个多项式时间算法
-
迄今为止不能排除 NP 完全问题实际上可以在多项式时间内求解的可能性
-
已知的NP完全问题:
- 确定是否在给定数量的边中包含一条简单路径
- 确定一个有向图/无向图中是否包含哈密顿圈
- 证明一个3-CNF布尔表达式是否是可满足的

Let’s start with an example: The problem solving a Sudoku puzzle. It’s very easy to quickly check a solution (i.e. you are given a solution and all you need to do is to scan through the rows, columns, and 3 x 3 cells to tell it is a valid solution: each of 1, 2, … , 9 must occur exactly once), but finding a solution from scratch might take a lot longer. To this day, the best methods we know for solving Sudoku puzzles essentially amount to systematically trying all possibilities. Thus,we can say that “Finding a solution to a problem is harder than checking that a solution”. There are several such problems in the real world that can be checked(verified) easily but cannot be solved easily(As of now, there is no easy solution, in future someone may come up with some easy algo or someone may be prove that there is no easy solution ). There are obviously lots of problems in the real world that can be/are solved easily!
So, we can think in this way, some problems can be solved easily and some problems can be checked/verified(with a given solution) easily.
The class of problems that can be solved easily are called P-problems.
The class of problems that can be verified easily are called NP-problems.
Now, a problem that can be solved easily can be also verified easily(Think intuitively, as solving is more difficult than verifying, so if the more difficult task can be done easily, then the easier task can be obviously done easily!). E.g: You are asked to sort an array,so you are finding the sorted array, that’s easy. Also, if you are given a sorted array and asked to verify it, that’s easy too Hence, all problems that can be solved easily can be verified easily. So, All P problems are NP problems.
But, if any problem can be only verified easily, we may or may not be able to solve it easily.Take the example of Sudoku:only verifying is easy,solving is not easy(At least as of now, easy solution is not known, in future some one may come up with an easy solution). So, All NP problems are not P problems.
P is a subset of NP.
Another way of saying this is, NP problems(problems that can be verified easily) that can be also solved easily are called P problems.
A very important thing, understand, for P problems there is easy verification as well as easy solution ,for the NP problems that are not in P, i.e. problems for which only easy verification is known but easy solving is not known, it cannot be said that they have or don’t have easy solution. Whether they have or do not have easy solution is still not known. Someone may be able to prove in future that the problem has an easy solution or someone may prove that the problem does not have easy solution, it only has easy verification.
Thus:
We are sure that all P problems can be both easily verified and easily solved.
But for NP problems, we just know that they can be easily verified. We don’t know still if they can be easily solved or not.
When will NP be equal to P?
-when we will get easy solution for all NP problems (particularly, the NP-P problems)
Instead of trying to find out every NP problem will have an easy solution or not(that’s a mammoth task you see!!), let us consider one single problem ‘X’ that is as hard as every NP problem, and then try to find whether ‘X’ has an easy solution or not. If X can be solved easily, then that means every problem in NP can be solved easily. (Remember, X should be easily derivable/reducible from the NP problems,otherwise if derivation/reduction itself is hard, then the other findings of easiness/hardness are of no use!)
Easily solved problem means a P problem.
Thus if it’s proved that every NP problem can be easily solved, it will lead to the fact that P=NP .
How will we able to prove that NP cannot be equal to P?
If any NP problem can be proved that it cannot be solved easily,then that means there is at least one problem that cannot be solved easily.There is at least one problem in NP-P part. This will prove that P !=NP.
What is NP-hard problem?
The problem X that we can considered earlier, which should be as hard as every NP problem, so that easy solution for X will give easy solution for every NP problem is called NP-hard problem. Such problems should be easily reducible from the NP problems, only then it will be considered.
What is NP-complete problem? An NP-hard problem which is also in NP is called NP-complete, that is , one of the NP problems is as hard as every other problem in NP,and solving that problem will solve all NP problems.
Thus:
if an NP-hard or NP-complete problem is proven to have an easy solution,then it will lead to the fact : NP=P
if any NP( or NP-complete) problem is proven to not have an easy solution, then it will lead to the fact that : NP!=P