Red-Black Trees and B+ Trees

Red-Black Trees

• Target: Balanced binary search tree

[Definition] A red-black tree is a binary search tree that satisfies the following red-black properties:

• Every node is either red or black
• The root is black
• Every leaf (NIL) is black
• If a node is red, then both its children are black
• For each node, all simple paths from the node to descendant leaves contain the same number of black nodes

[Definition] The black-height of any node $x$, denoted by $\text{bh}(x)$, is the number of black nodes on any simple path from $x$ ($x$ not included) down to a leaf.

• $\text{bh}(\text{Tree}) = \text{bh}(\text{root})$

[Lemma] A red-black tree with $N$ internal nodes has height at most $2\ln(N +1)$.

• For any node $x$, $\text{sizeof}(x) \geq 2^{\text{bh}(x)} – 1$. Proved by induction.
• $\text{bh}(\text{Tree}) \geq \text{h}(\text{Tree}) / 2$ (一条从根结点到叶结点的路径上最多有一半是红色结点，否则会有两个红色结点相邻)

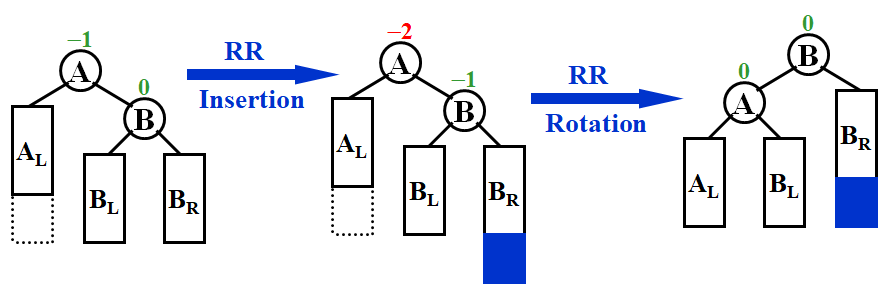
Insert

• 插入的结点设为红色

• $T=O(h)=O(\ln N)$

Delete

• Delete a leaf node: Reset its parent link to NIL and adjust only if the node is black
• Delete a degree 1 node: Replace the node by its single child
• Delete a degree 2 node:
  • Replace the node by the largest one in its left subtree or the smallest one in its right subtree
  • Delete the replacing node from sub tree
• Must add 1 black node to the path of the replacing node.

Note: $x$ is the location of the node to be deleted initially, and a black node needs to be added to the path of $x$.

Red-Black Trees VS AVL Trees

• Number of rotations

	Red-Black Trees	AVL Trees
Insertion	$\leq2$	$\leq2$
Deletion	$\leq3$	$O(\log N)$

• AVL Trees is faster for search time because the tree height is smaller.

B+ Trees

[Definition] A B+ tree of order $M$ is a tree with the following structural properties:

• The root is either a leaf or has between $2$ and $M$ children.
• All nonleaf nodes (except the root) have between $\lceil M/2\rceil$ and $M$ children.
• All leaves are at the same depth.

Note: Assume each nonroot leaf also has between $\lceil M/2\rceil$ and $M$ children.

• All the actual data are stored at leaves
• Each interior node contains $M$ pointers to the children, and $M-1$ smallest key values in the subtrees except the first one.
• Deletion is similar to insertion except that the root is removed when it loses two children.

Btree Insert ( ElementType X,  Btree T ) 
{ 
	Search from root to leaf for X and find the proper leaf node;
	Insert X;
	while ( this node has M+1 keys ) 
	{
    	split it into 2 nodes with \lceil(M+1)/2\rceil and \lfloor(M+1)/2\rfloor keys, respectively;
    	if (this node is the root)
        	create a new root with two children;
    	check its parent;
	}
} 

$\text{Depth}(M,N)=O(\lceil\log_{\lceil M/2\rceil}N\rceil)$

$T_\text{Find}(M,N)=O(\log N)$

Note: The best choice of $M$ is 3 or 4.