OE.Heart's Blog

Parallel Random Access Machine (PRAM) To resolve access conflicts Exclusive-Read Exclusive-Write (EREW) Concurrent-Read Exclusive-Write (CREW) Concurrent-Read Concurrent-Write (CRCW) Arbitrary rule Priority rule (P with the smallest number) Common rule (if all the processors are trying to write the same value) The summation problem Input: A(1),A(2),⋯ ,A(n)A(1), A(2), \cdots, A(n)A(1),A(2),⋯,A(n) Output: $ A(1) + A(2) + \cdots +A(n)$ B(h,i)=B(h−1,2i−1)+B(h−1,2i)B(h, i) = B(h-1, 2i-1) ...

Introduction What to Randomize The world behaves randomly – randomly generated input solved by traditional algorithm Average-case Analysis The algorithm behaves randomly – make random decisions as the algorithm processes the worst-case input Randomized Algorithms Why Randomize Efficient deterministic(确定性) algorithms that always yield the correct answer are a special case of – efficient randomized algorithms that only need to yield the correct answer with high probability randomize ...

Introduction Solve problems approximately - aims at a local optimum Framework of Local Search Local Define neighborhoods in the feasible set A local optimum is a best solution in a neighborhood Search Start with a feasible solution and search a better one within the neighborhood A local optimum is achieved if no improvement is possible Neighbor Relation S ~ S’: ​S’​ is a neighboring solution of S, S’ can be obtained by a small modification of S N(S): neighborhood of S, the set { ...

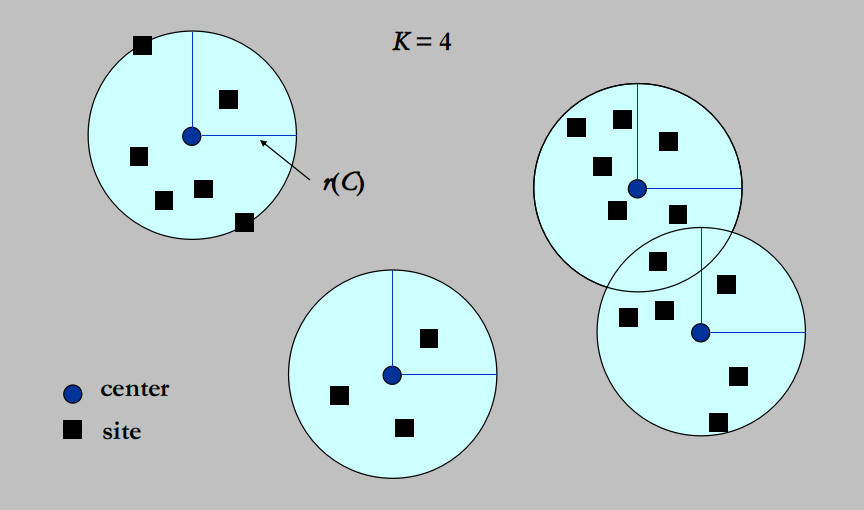
Introduction Dealing with HARD problems Getting around NP-completeness If NNN is small, even O(2N)O(2^N)O(2N) is acceptable Solve some important special cases in polynomial time Find near-optimal solutions in polynomial time — approximation algorithm Note: greedy 等 heuristics 不管效果，approximation 有近似解的质量方面的讨论 Approximation Ratio [Definition] An algorithm has an approximation ratio of ρ(n)\rho(n)ρ(n) if, for any input of size nnn, the cost CCC of the solution produced by the algorithm is ...

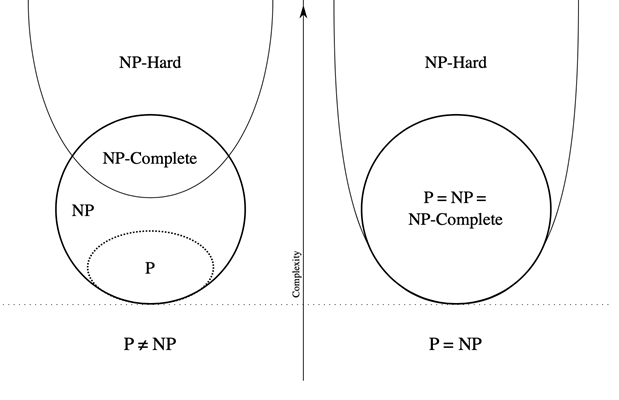
NP 类问题指在多项式时间内可以被证明的问题 所有的 P 类问题同时也是 NP 类问题，即 P⊆NPP\subseteq NPP⊆NP P 类问题是否是 NP 类问题的真子集在目前是一个开放问题 如果一个 NP 问题和其它任何 NP 问题一样“不易解决”，则认为这一问题是 NP 完全问题 如果任何 NP 完全问题可以在多项式时间内解决，则所有 NP 问题都有一个多项式时间算法 迄今为止不能排除 NP 完全问题实际上可以在多项式时间内求解的可能性 已知的NP完全问题： 确定是否在给定数量的边中包含一条简单路径 确定一个有向图/无向图中是否包含哈密顿圈 证明一个3-CNF布尔表达式是否是可满足的 Let’s start with an example: The problem solving a Sudoku puzzle. It’s very easy to quickly check a solution (i.e. you are given a solution and all you need to do is to scan throu ...

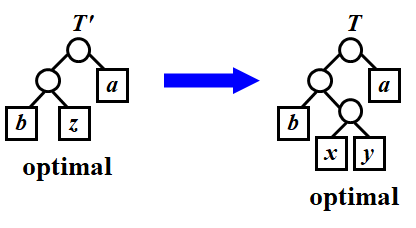
Introduction Optimization Problems: Given a set of constraints and an optimization function. Solutions that satisfy the constraints are called feasible solutions. A feasible solution for which the optimization function has the best possible value is called an optimal solution. The Greedy Method: Make the best decision at each stage, under some greedy criterion. A decision made in one stage is not changed in a later stage, so each decision should assure feasibility. Note: Greedy algorithm w ...

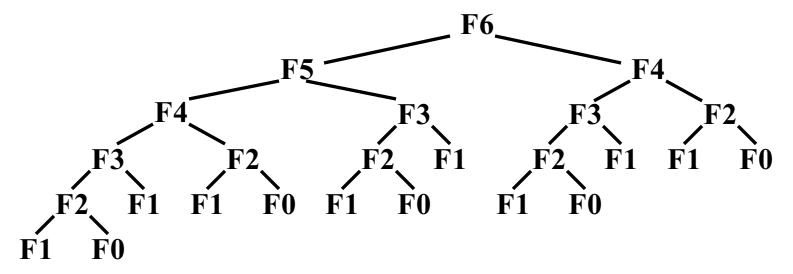
Solve sub-problems just once and save answers in a table Use a table instead of recursion Fibonacci Numbers F(N)=F(N−1)+F(N−2)F(N)=F(N-1)+F(N-2) F(N)=F(N−1)+F(N−2) 12345int Fib(int N) { if (N <= 1) return 1; else return Fib(N-1)+Fib(N-2); } T(N)≥T(N−1)+T(N−2)→T(N)≥F(N)T(N)\geq T(N-1)+T(N-2)\rarr T(N)\geq F(N) T(N)≥T(N−1)+T(N−2)→T(N)≥F(N) Trouble maker: The growth of redundant calculations is explosive. Solution: Record the two most recently computed values to avoid recu ...

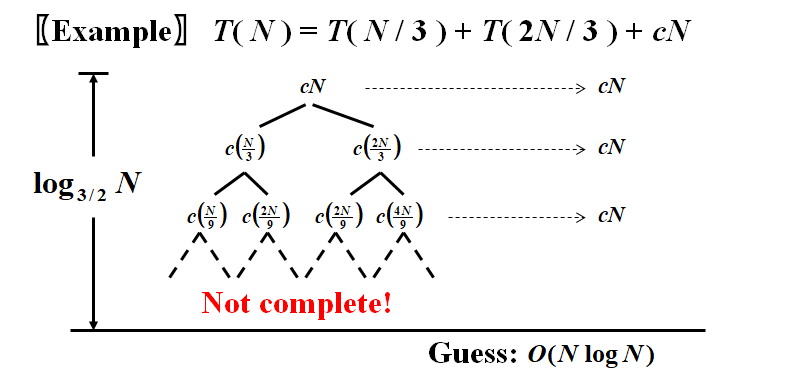
Introduction Recursively: Divide the problem into a number of sub-problems Conquer the sub-problems by solving them recursively Combine the solutions to the sub-problems into the solution for the original problem General recurrence: T(N)=aT(N/b)+f(N)T(N)=aT(N/b)+f(N)T(N)=aT(N/b)+f(N) Cases solved by divide and conquer The maximum subsequence sum – the O(Nlog⁡N)O( N\log N )O(NlogN) solution Tree traversals – O(N)O( N )O(N) Mergesort and quicksort – $O( N\log N ) $ Closest Points Pr ...

Rationale of the Backtracking Algorithms A sure-fire way to find the answer to a problem is to make a list of all candidate answers, examine each, and following the examination of all or some of the candidates, declare the identified answer If the list is finite and it is possible to identify the answer following the examinations. And, if there are not too many candidates Backtracking enables us to eliminate the explicit examination of a large subset of the candidates while still guarante ...

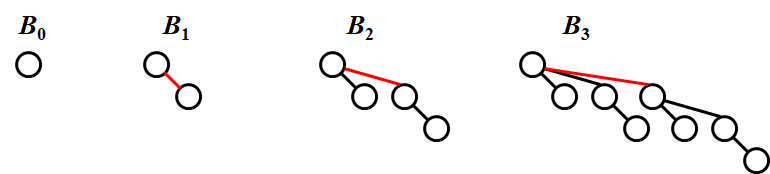
Structure A binomial queue is not one heap-ordered tree, but rather a collection of heap-ordered trees, known as a forest. Each heap-ordered tree is a binomial tree. A binomial tree of height 0 is a one-node tree. A binomial tree, BkB_kBk​, of height kkk is formed by attaching a binomial tree,Bk–1B_{k – 1}Bk–1​, to the root of another binomial tree, Bk–1B_{k – 1}Bk–1​. BkB_kBk​ consists of a root with kkk children, which are B0,B1,⋯ ,Bk−1B_0,B_1,\cdots,B_{k-1}B0​,B1​,⋯,Bk−1​. BkB_kBk​ h ...